paul lawitzki
software developer and game designerMath Fundamentals: Rotation Matrices
The mathematical representation of rotations is a key subject for many technical applications. Especially in physics simulations, game programming or the processing of geometric sensor data a basic understanding of mathematical concepts like rotation matrices or quaternions is required. This article imparts some essential principles of rotation matrices by deriving a general rotation matrix in 3d-space from the trigonometric functions. Rotations performed with such a rotation matrix take the Euler angles as parameters.
All three-dimensional vectors and matrices in this article follow the right-handed coordinate system convention (x-axis: east; y-axis: north; z-axis: up).
Two-Dimensional Rotation Matrices
As a first approach to the topic the general two-dimensional rotation matrix is derived from the basic trigonometric functions (sine and cosine). We're in the following initial situation: There is a point $\overrightarrow{p}$, which can be described as a two-domensional vector, and an angle β by which $\overrightarrow{p}$ will be rotated around the origin (0, 0). The rotation operation yields a vector $\overrightarrow{p}_{rot}$. How is the rotation operation defined?
Let's break down the information available to us:
Since $\overrightarrow{p}_{rot}$ is $\overrightarrow{p}$ rotated by an angle β around the origin, the distances between $\overrightarrow{p}$ and the origin and $\overrightarrow{p}_{rot}$ and the origin are the same. The two vectors have the same magnitude:
$$|\overrightarrow{p}_{rot}|=|\overrightarrow{p}|$$We define the angle between the x-axis and the vector $\overrightarrow{p}$ as α. Both components of $\overrightarrow{p}$, x and y, can be described as trigonometric functions of α multiplied by $\overrightarrow{p}$'s magnitude:
$$ \overrightarrow{p} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} |\overrightarrow{p}|\cos{\alpha} \\ |\overrightarrow{p}|\sin{\alpha} \end{pmatrix} $$The same kind of description can be provided for $\overrightarrow{p}_{rot}$. But since $\overrightarrow{p}_{rot}$ is $\overrightarrow{p}$ rotated by β, its components $x_{rot}$ and $y_{rot}$ are trigonometric functions of (α+β):
$$ \overrightarrow{p}_{rot} = \begin{pmatrix} x_{rot} \\ y_{rot} \end{pmatrix} = \begin{pmatrix} |\overrightarrow{p}_{rot}|\cos{(\alpha + \beta)} \\ |\overrightarrow{p}_{rot}|\sin{(\alpha + \beta)} \end{pmatrix} $$This situation can be summarized in the following picture:
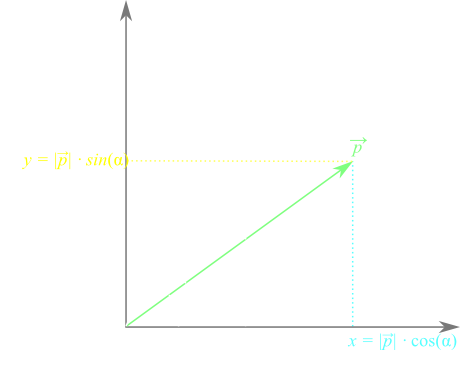
Now that we have established a relation between the components of our target vector $\overrightarrow{p}_{rot}$ and the given angles, we need to find out how the initial vector $\overrightarrow{p}$ fits into the equation. Our goal is to find an expression which yields the target vector and which depends solely on the initial two components x and y and the rotation angle β. In order to do this, we need to separate the sum of α and β in the trigonometric functions. We can achieve this with the fundamental formulas of angle addition in trigonometry:
$$ \sin{(a\pm b)} = \sin{a}\cos{b}\pm\cos{a}\sin{b}\\ \cos{(a\pm b)} = \cos{a}\cos{b}\mp\sin{a}\sin{b} $$If we apply these formulas on our previous description of $\overrightarrow{p}_{rot}$ we get the following term:
$$ \begin{pmatrix} x_{rot} \\ y_{rot} \end{pmatrix} = \begin{pmatrix}|\overrightarrow{p}|\cos{(\alpha+\beta)} \\ |\overrightarrow{p}|\sin{(\alpha+\beta)}\end{pmatrix}= \begin{pmatrix} |\overrightarrow{p}|\cos{\alpha}\cos{\beta}-|\overrightarrow{p}|\sin{\alpha}\sin{\beta} \\ |\overrightarrow{p}|\sin{\alpha}\cos{\beta}+|\overrightarrow{p}|\cos{\alpha}\sin{\beta} \end{pmatrix} $$Upon closer inspection, we can recognize thas some parts of this expression are x and y, the components of the initial vector $\overrightarrow{p}$:
$$ \begin{pmatrix} x_{rot} \\ y_{rot} \end{pmatrix} = \begin{pmatrix}|\overrightarrow{p}|\cos{(\alpha+\beta)} \\ |\overrightarrow{p}|\sin{(\alpha+\beta)}\end{pmatrix}= \begin{pmatrix} \overbrace{|\overrightarrow{p}|\cos{\alpha}}^{x}\cos{\beta}-\overbrace{|\overrightarrow{p}|\sin{\alpha}}^{y}\sin{\beta} \\ \underbrace{|\overrightarrow{p}|\sin{\alpha}}_{y}\cos{\beta}+\underbrace{|\overrightarrow{p}|\cos{\alpha}}_{x}\sin{\beta} \end{pmatrix} $$We can substitute these parts with x and y. Notice that all trigonometric functions containing α are now gone. Or goal is to single out the initial vector $\overrightarrow{p}$ in this equation. The last part of the previous equation can be written down as the product of the two-dimensional vector $\overrightarrow{p}$ and a 2×2 matrix:
$$ \begin{pmatrix} x_{rot} \\ y_{rot} \end{pmatrix} = \begin{pmatrix}x\cos{\beta} - y\sin{\beta} \\ x\sin{\beta} + y\cos{\beta}\end{pmatrix}= \underbrace{\begin{pmatrix}\cos{\beta} && -\sin{\beta} \\ \sin{\beta} && \cos{\beta}\end{pmatrix}}_{R} \underbrace{\begin{pmatrix}x \\ y\end{pmatrix}}_{\overrightarrow{p}} $$Now we have established the relationship between the vector $\overrightarrow{p}$, the angle β and the rotated vector $\overrightarrow{p}_{rot}$. The Rotation can be expressed as the product with the 2×2 matrix R:
$$ \overrightarrow{p}_{rot} = R\overrightarrow{p} \\ R=\begin{pmatrix}\cos{\beta} && -\sin{\beta} \\ \sin{\beta} && \cos{\beta}\end{pmatrix} $$Notice that the multiplication $R\overrightarrow{p}$ is not commutative. Since it is a matrix multiplication, the order in which the multiplication is performed makes a difference. However, in this case the result of the multiplication $\overrightarrow{p}R$ is not defined because of the dimensions of the two factors. Rotation matrices are always multiplied from the left side with the vector to be rotated.
Three-Dimensional Rotation Matrices
The next step is to continue the above thoughts in three-dimensional space. As soon as we add a third dimension, we realize that there is more than one angle by which we can rotate a vector. In fact we have three orthogonal axes about which a rotation can be performed. Every single rotation in 3D space can be described as a compound of three rotations about the three axes x, y and z.
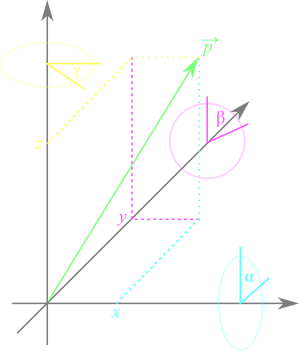
Now that our vectors have three components, we require a 3×3 matrix to describe a rotation:
$$ \overrightarrow{p}_{rot} = \begin{pmatrix}x_{rot} \\ y_{rot} \\ z_{rot}\end{pmatrix}= R\overrightarrow{p}=\begin{pmatrix}R_{11} && R_{12} && R_{13} \\ R_{21} && R_{22} && R_{23} \\ R_{31} && R_{32} && R_{33}\end{pmatrix}\begin{pmatrix}x \\ y \\ z\end{pmatrix} $$First, in order to construct the general rotation matrix we need to look at each rotation axis separately. If, for example, the vector $\overrightarrow{p}$ is rotated about the x-axis (by an angle α), not all of its components are affected by the rotation. The x-component is located on the roatation axis, thus the value of x remains the same for any given angle α. The same principle applies for the other two rotation axes and the respective components of $\overrightarrow{p}$. If we describe three vectors, each the result of a rotation of $\overrightarrow{p}$ about an axis of the coordinate system (i.e. $\overrightarrow{p}_x$ is $\overrightarrow{p}$ rotated about the x-axis etc.) we can predict that only the components on the axes orthogonal to the rotation axis are affected:
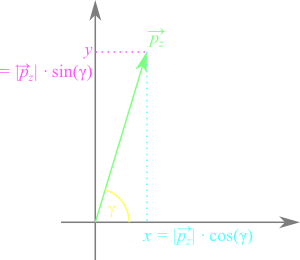
$$ \overrightarrow{p}_{x}=\begin{pmatrix}x \\ y_{rot} \\ z_{rot}\end{pmatrix}; \overrightarrow{p}_{y}=\begin{pmatrix}x_{rot} \\ y \\ z_{rot}\end{pmatrix}; \overrightarrow{p}_{z}=\begin{pmatrix}x_{rot} \\ y_{rot} \\ z\end{pmatrix} $$Now we are able to determine the rotation matrix for each of the above vectors. The angles $\alpha_0$, $\beta_0$ and $\gamma_0$ are the initial angles of $\overrightarrow{p}$ whereas α, β and γ are the angles by which $\overrightarrow{p}$ is rotated. For the rotation about the x-axis we only need to consider the z-y-plane, since x remains unchanged:
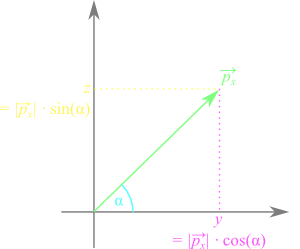
The following steps are the same as in the two-dimensional case: Describe the affected vector components as trigonometric functions to establish a relationship with the angle. Then, apply the trigonometric addition formulas to get rid of the additions within the trigonometric functions. Identify the initial components in the trigonometric expressions and substitute them to get a shorter form. Finally, deduce the rotation matrix.
$$ \overrightarrow{p}_{x}= \begin{pmatrix}x \\ |\overrightarrow{p}_{x}|\cos{(\alpha_0+\alpha)} \\ |\overrightarrow{p}_{x}|\sin{(\alpha_0+\alpha)}\end{pmatrix}= \begin{pmatrix}x \\ |\overrightarrow{p}_{x}|\cos{\alpha_0}\cos{\alpha}-|\overrightarrow{p}_{x}|\sin{\alpha_0}\sin{\alpha} \\ |\overrightarrow{p}_{x}|\cos{\alpha_0}\sin{\alpha}+|\overrightarrow{p}_{x}|\sin{\alpha_0}\cos{\alpha}\end{pmatrix}= \begin{pmatrix}x \\ y\cos{\alpha}-z\sin{\alpha} \\ y\sin{\alpha}+z\cos{\alpha}\end{pmatrix} $$ $$ \overrightarrow{p}_{x}= \underbrace{\begin{pmatrix} 1 && 0 && 0 \\ 0 && cos{\alpha} && -\sin{\alpha} \\ 0 && \sin{\alpha} && \cos{\alpha}\end{pmatrix}}_{R_x} \underbrace{\begin{pmatrix}x \\ y \\ z\end{pmatrix}}_\overrightarrow{p}=R_x\overrightarrow{p} $$We use the same approach for the rotation about the y-axis. However, there is one detail to the y-axis rotation we need to bear in mind. For each axis-rotation we change our viewpoint, so we are looking in the opposed direction of the rotation axis vector. In the case of y-axis rotation, we look at the x-z-plane and the x-axis is flipped. As a result the rotation angle β is inverted and we need to change its sign:
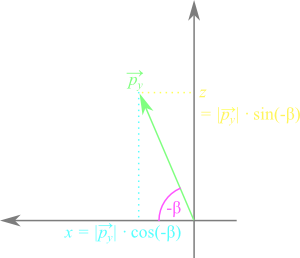
The same approach for the z-axis rotation. This time there are no flipped axes, so this case is analogous to the x-axis rotation:
Now, we have established the matrices for all three elemental rotation about each of the three axes of the coordinate system. If we would like to apply a rotation including all three euler angles, we could combine the three matrices by multiplying them. Note that the order in which the matrices are multiplied does matter. Matrix multiplications (and thus rotation operations) are not commutative. We have to define a convention for the order in which the elemental rotations are applied. Once this convention is established all rotations should follow it for the sake of consistency. Rotation matrices are multiplied from right to left. So, if the rotation order is x-y-z the three matrix multiplications are applied as follows:
$$ \overrightarrow{p}_{rot}= R\overrightarrow{p} = R_z R_y R_y\overrightarrow{p} =\\ \underbrace{\begin{pmatrix}\cos{\gamma} && -\sin{\gamma} && 0 \\ \sin{\gamma} && \cos{\gamma} && 0 \\ 0 && 0 && 1\end{pmatrix} \underbrace{\begin{pmatrix}\cos{\beta} && 0 && \sin{\beta} \\ 0 && 1 && 0 \\ -sin{\beta} && 0 && \cos{\beta}\end{pmatrix} \underbrace{\begin{pmatrix}1 && 0 && 0 \\ 0 && \cos{\alpha} && -\sin{\alpha} \\ 0 && \sin{\alpha} && \cos{\alpha}\end{pmatrix} \begin{pmatrix}x \\ y \\ z \end{pmatrix}}_{\text{1st roation about x-axis}}}_{\text{2nd rotation about y-axis}}}_{\text{3rd rotation about z-axis}} $$Finally, the three elemental rotation matrices can be summarized in one rotation matrix:
$$ R = R_z R_y R_x \\ = \begin{pmatrix} \cos{\beta}\cos{\gamma} && \sin{\alpha}\sin{\beta}\cos{\gamma}-\cos{\alpha}\sin{\gamma} && \sin{\alpha}\sin{\gamma}+\cos{\alpha}\sin{\beta}\cos{\gamma} \\ \cos{\beta}\sin{\gamma} && \sin{\alpha}\sin{\beta}\sin{\gamma}+\cos{\alpha}\cos{\gamma} && \cos{\alpha}\sin{\beta}\sin{\gamma}-\sin{\alpha}\cos{\gamma} \\ -\sin{\beta} && \sin{\alpha}\cos{\beta} && \cos{\alpha}\cos{\beta} \end{pmatrix} $$